Lineare Optimierung
Aufgabe 1:
Ein
Unternehmen produziert zwei Sorten Hundefutter: Produkt I: "Fodo", Produkt II: "
Bello ".
Pro Tag
können von den beiden höchstens 10 Stück hergestellt werden. Dafür stehen 6
Arbeiter zur Verfügung, die insgesamt höchstens 24 Stunden am Tag arbeiten
können. Zur Herstellung des Produkts I ( je für eine Packung) werden 4
Arbeitsstunden benötigt und zur Herstellung von Produkt II werden 2
Arbeitsstunden benötigt. Der Materialverbrauch in der Produktion kann aus
Kapazitätsgründen höchstens 40 ME betragen, wobei zur Herstellung von Produkt I
, für 1 Packung, 2 ME und für 1 Packung des Produktes 2 4 ME des benötigten
Materials eingesetzt werden muss. Das Produkt 1 kann das Unternehmen zu einem
Preis von 10 Euro/ Stück und das Produkt 2 zu einem Preis von 15 Euro/ Stück am
Markt absetzen.
|
Aufgabe
2:
 |
Um etwas
zu basteln braucht eine Klassengruppe unterschiedliche "Pappstreifen" bei
der folgende Stückzahlen zu verwenden sind:
-
6
Pappstreifen der Größe 1,
-
4 Pappstreifen der Größe 2,
-
10
Pappstreifen der Größe 3.
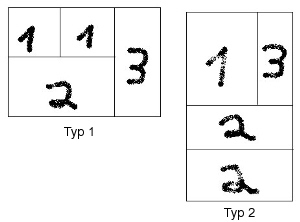
Dazu
holen sie sich 2 Typen von Pappkollagen aus einem Bastelladen, die auf
vorgegebene Weise zu zerschneiden sind.
|
Der
Preis einer Kollage des Typs 1 beträgt 5 Euro und der Preis einer Kollage
des Typs 2 beträgt 3 Euro.
Wie viele Kollagen von Typ 1 und 2 müssen gekauft werden, sodass der
Gesamteinkaufspreis so gering wie möglichst ausfällt?
[Jasmin
Singh, 11b, 2004]
Aufgabe 3:
Wir müssen ein Haus mit großen Räumen mit
Heizkörpern ausstatten, wozu 2 verschiedene Heizkörpertypen zur Auswahl stehen:
Heizkörper 1 gibt 1 kW ab, Heizkörper 2 gibt 2,5 kW ab. Es müssen jedoch
insgesamt 14 kW abgegeben werden. Wir müssen Typ 2 mindestens 2 mal verbauen.
Unser Kunde möchte ebenfalls, dass wir Typ 1 auch einbauen. Leider haben wir Typ
2 nur 4 mal, Typ 1
nur 9 mal auf Lager und können so kurzfristig nicht
nachbestellen. Der Kunde möchte außerdem, dass wir nicht mehr als 4.400 € für
alle Heizkörper brauchen.
(1) Geben Sie grafisch die Menge aller
Heizkörpertypen-Kombinationen an.
(2) Ein kleiner Heizkörper kostet 250,- €, ein
großer kostet 700,- €. Welche
Kombination verursacht die geringsten Kosten?
[Ingolf Kaifer, 11b, 2004]
Aufgabe 4:
Für
einen großen Kindergeburtstag sollen zwei verschiedene Sorten Süßigkeiten
eingekauft werden. Eine Tüte der ersten Sorte wird zu einem Preis von 3 €
angeboten und eine Tüte der zweiten Sorte kostet 4 €. Es dürfen aber nicht mehr
als 30 € ausgegeben werden. Von der ersten Sorte soll doppelt soviel wie von der
zweiten Sorte eingekauft werden. Von der zweiten Sorte sollen aber mindestens 4
Tüten eingekauft werden. Obwohl nicht mehr viel Platz im Einkaufswagen ist
können mindestens 38,5 Tüten Süßigkeiten eingekauft werden, wobei die erste
Sorte das Dreifache an Platz benötigt. Welche Kombination der beiden Sorten
verursacht die geringsten Kosten ?
Aufgabe 5:
Ein
Unternehmen stellt zwei Sorten von Christbaumkugeln her. Zur Herstellung der
zweiten Sorte werden 2 g. Glas mehr verbraucht als zur Herstellung der ersten
Sorte und insgesamt werden höchstens 12 g. Glas benötigt. Die erste Sorte kostet
5 € und die zweite Sorte 8 €. Es werden 7 Arbeitsstunden zur Herstellung der
ersten Sorte benötigt und für die zweite Sorte vier Arbeitsstunde weniger, an
einem Arbeitstag dürfen höchstens 17 Stunden gearbeitet werden. An einem
Arbeitstag werden insgesamt höchstens 16 Christbaumkugeln hergestellt, wovon
höchstens 13 zu der zweiten Sorte gehören. Welche Produktionsmöglichkeit der
beiden Produkte bringt den höchsten Umsatz ?
[Hanne Timm, 11b, 2004]
Aufgabe 6:
Das Unternehmen „Lowrider“ stellt Hydraulikpumpen
(HP) für Automobile her. „Lowrider“ baut 2 verschiedene Typen der HP (Stufe1 und
Stufe2). Die Kosten für die Produktion von Stufe1 belaufen sich auf 1.000 €/St.
und bei Stufe2 auf 3.000 €/St.. Am Tag darf nicht mehr als 30.000 € für die
Produktion ausgegeben werden.
Die Herstellung dauert bei Stufe1 20Std./Tag und bei
Stufe2 60 Std./Tag. Es stehen maximal 510 Std. für die Herstellung zur
Verfügung. Von Stufe1 sollen maximal 6 Stück am Tag hergestellt werden; von
Stufe2 mindestens 4 Stück. Verkauft wird Stufe1 für 2.000 €/St. und Stufe2 für
6.000 €/St.
Der Umsatz soll maximiert werden!
Aufgabe 7:
Ein Familienbetrieb stellt zwei Anzüge aus
verschiedenen Stoffen her. Die Produktionskosten belaufen sich bei Anzug 1 auf
5.000 €/St. Und bei Anzug 2 auf 3.000 €/St..
Pro Tag steht höchstens 30.000 € für die Produktion
zur Verfügung. Die Herstellung für
Anzug1 dauert 30 Std. und für Anzug2 60 Std. Maximal
stehen 480 Std. für die Herstellung am Tag zur Verfügung. Von Anzug1 sollen
höchstens 3 Stück angefertigt werden. Aus Erfahrung weiß man, dass sich von
Anzug2 mindestens 4 Stück am Tag verkaufen lassen.
Verkauft wird Anzug1 für 10.000 €/St. Und Anzug2 für
5.000 €/St..
Der Umsatz soll maximiert werden!
[Gerrit Jochims, 11b, 2004]
Aufgabe 8:
Ein Unternehmen produziert zwei verschiedene
Personenkraftwagen (PkW). Einer der PkWs ist ein Kleinwagen, der andere PkW ist
ein Kombi. Das Unternehmen kann höchstens 10 PkWs täglich herstellen. Ein
Kleinwagen wird auf einem Laufband produziert und ein Kombi wird auf zwei
Laufbändern hergestellt. Dem Unternehmen stehen höchstens 14 Laufbänder zu
Verfügung. Wegen dem so genannten Lagerparkplatz können nicht mehr als 6 der
Kleinwagen und nicht mehr als 7 der Kombiwagen produziert werden. Der Preis des
Kleinwagen beträgt 8.000 € und der des Kombis beträgt 10.000 €.
Welche Mengenkombination der zwei Pkws muss das
Unternehmen verkaufen um den maximalen Umsatz erzielen zu können?
Aufgabe 9:
Eine Tischlerei produziert u. A. große und kleine
Schränke. Die Herstellung eines kleinen Schranks verursacht Kosten in Höhe von
800 € und die Produktion eines großen Schranks verursacht Kosten in Höhe von
1000 €. Für die Herstellung der Schränke werden jeweils für einen kleinen
Schrank mindestens zwei Arbeitsstunden und für einen großen Schrank mindestens
drei Arbeitsstunden benötigt. Die Tischlerei arbeitet 8 Stunden täglich.
Diese Tischlerei erhält einen Auftrag:
Es sollen mindestens 14 Schränke geliefert werden.
Aber es dürfen nicht mehr als 7 kleine Schränke und nicht mehr als 11 große
Schränke zugestellt werden.
Für die Erfüllung des Auftrags muss die Tischlerei
mindestens 3 Arbeitstage einrechnen. Welche Kombination der zwei Schränke muss
die Tischlerei herstellen um den Auftrag erfüllen zu können und die Kosten so
gering wie möglich zu halten?
[Irina Hensler, 11b, 2004]
Aufgabe 10:
Ein Unternehmen stellt 2
Sorten von Fahrrädern her. Es können höchstens 35 Fahrräder beider Sorten pro
Tag hergestellt werden. Es werden mindestens 10 Fahrräder pro Tag hergestellt.
Sorte 1 braucht 4 Stunden zur Herstellung und Sorte 2 braucht 2 Stunden zur
Herstellung eines Stückes. Das Unternehmen hat 10 Mitarbeiter für diese Arbeit
eingestellt, die höchstens insgesamt 112 Stunden pro Tag arbeiten. Sorte 1 der
Fahrräder nimmt 2qm des Lagers in Anspruch und Sorte 2 benötigt 4qm Platz für
ein Fahrrad. Insgesamt ist das Lager 120qm groß. Sorte 1 kostet 100 EUR/Stk. Und
Sorte 2 kostet 80 EUR/Stk. .
Welche
Produktionsmöglichkeiten der beiden Produkte gibt es, damit der Gewinn maximiert
wird?
Aufgabe 11:
Ein Unternehmen stellt
kostbare Teppiche her. Einmal große Teppiche und kleine Teppiche. Für die
Herstellung eines großen Teppichs brauchen die Mitarbeiter 10 Stunden und für
die Herstellung eines kleinen Teppichs werden 5 Stunden benötigt. Es wird aber
nur insgesamt 20 Stunden gearbeitet. Da nur ein kleines Lager vorhanden ist und
die Nachfrage nicht sonderlich groß ist, werden insgesamt 3 Teppiche beider
Sorten pro Tag hergestellt. Die großen Teppiche bringen 2000 EUR/Stk. ein und die
kleinen bringen 750 EUR/Stk. ein
[Sarah Schöbel, 11b, 2004]
Aufgabe 12:
Ein Landwirt
besitzt 100 Morgen Land und hat 200 Arbeitstage im Jahr zur Verfügung, um dieses
Land zu bewirtschaften. Er entscheidet sich für den Anbau von Weizen und Gemüse,
die pro Morgen einen Arbeitsaufwand von 1 Tag bzw. 4 Tagen verlangen. Für die
Bebauung kann er höchstens 12.000 EUR Kapital aufwenden. Der Kapitalaufwand pro
Morgen Weizen beträgt 100 EUR, der für Gemüse 200 EUR.
Der Landwirt möchte
maximalen Gewinn erzielen, wobei er pro Morgen Weizen mit einem Gewinn von 40
EUR und bei einem Morgen Gemüse mit einem Gewinn von 120 EUR rechnet (Gewinn =
Erlös - Unkosten)
Aufgabe 13:
Ein Kaffeehändler
will 2 Sorten Kaffee einkaufen, eine teuere Sorte A und eine billigere
Sorte B. Von der Sorte A kann er höchstens 120 kg, von der Sorte
B höchstens 180 kg bekommen. Aus diesen beiden Sorten stellt er 2
Mischungen her: Die erste Mischung soll 20% der Sorte A und 80% der Sorte
B, die zweite Mischung soll 60% der Sorte A und 40% der Sorte B
enthalten. Der Verkaufspreis der ersten Mischung beträgt 12 EUR, der zweiten
Mischung 16 EUR je Kilogramm. Welche Menge muss der Händler von jeder Mischung
herstellen, damit er einen möglichst hohen Erlös erreicht?
Aufgabe 14:
Ein Gärtner läßt
den Boden auf die notwendigen Düngemittel untersuchen. Die Bodenproben ergeben,
dass 12 dz Kalidünger, 12 dz Phosphordünger, 15 dz Stickstoffdünger erforderlich
sind. Zur Verfügung stehen 2 Volldünger, die die Bestandteile in folgenden
Mengen enthalten:
1 Ladung Volldünger
I enthält 4 dz Kali, 3 dz Phosphor, 3 dz Stickstoff. 1 Ladung Volldünger II
enthält 2 dz Kali, 3 dz Phosphor, 6 dz Stickstoff. Der Preis von Volldünger I
beträgt 120 EUR/Ladung, von Volldünger II 80 EUR/Ladung. Welche Mengen muss der
Gärtner von jedem Dünger kaufen, damit dem Boden die notwendigen Bestandteile
zugeführt werden und die Gesamtkosten minimal sind?
Aufgabe 15:
Ein
landwirtschaftlicher Weidebetrieb hat sich auf die Haltung von Kühen und
Jungvieh spezialisiert. In den Ställen des Betriebes können höchstens 70 Kühe
und 500 Stück Jungvieh gehalten werden. Für die Ernährung einer Kuh sind 0,25
ha, für ein Stück Jungvieh 0,10 ha Weideland nötig. Insgesamt hat der Betrieb 50
ha Weideland. Für die Pflege der Kühe und des Jungviehes stehen 3 Arbeiter zur
Verfügung, die insgesamt 8.000 Arbeitsstunden im Jahr leisten. Für eine Kuh sind
100 Arbeitsstunden, für ein Stück Jungvieh 10 Arbeitsstunden je Jahr notwendig.
Der Gewinn bei einer Kuh beträgt 400 EUR, bei einem Stück Jungvieh 50 EUR im
Jahr.
Wie viele Kühe und
wie viel Stück Jungvieh muss der Betrieb halten, damit der Gesamtgewinn
möglichst groß wird?
Aufgabe 16:
Ein Gemüsebauer hat
insgesamt 30 Morgen Land zum Anbau von Erbsen und Stangenbohnen zur Verfügung.
Für einen Morgen Erbsen muss der Betrieb im Durchschnitt einen Arbeitstag, für
einen Morgen Stangenbohnen zwei Arbeitstage aufwenden. Insgesamt kann mit 50
Arbeitstagen gerechnet werden. Die Ausgaben für Saatgut betragen für einen
Morgen Erbsen 200 EUR, für einen Morgen Stangenbohnen 100 EUR. Der Bauer kann
höchstens 5000 EUR für das Saatgut ausgeben. Wie viel Morgen Erbsen und
Stangenbohnen muss der Bauer anbauen, damit sein Gewinn möglichst groß ist,
wobei der Gewinn bei einem Morgen Erbsen 200, bei einem Morgen Stangenbohnen 300
EUR beträgt?
Aufgabe 17:
Eine
Baugesellschaft hat ein Grundstück von 12.000 m² erworben. Darauf sollen 2- und
3stöckige Häuser gebaut werden, die 2stöckigen mit Garten, die 3stöckigen ohne
Garten. Die 2stöckigen Häuser sind für je 15 Personen, die 3stöckigen für je 21
Personen bestimmt. Die Kosten betragen bei einem zweistöckigen Haus 200.000 EUR,
bei einem dreistöckigen Haus 300.000 EUR. Insgesamt hat die Gesellschaft ein
Kapital von 6.000.000 EUR für den Bau der Häuser zur Verfügung. Für ein
zweistöckiges Haus wird eine Grundstücksfläche von 600 m², für ein dreistöckiges
von 400 m² benötigt. Die Anzahl der Arbeitsstunden zum Bau eines zweistöckigen
Hauses beträgt 6.000, bei einem dreistöckigen 12.000. Es können höchstens 228.000
Stunden aufgebracht werden. Nach dem Bebauungsplan dürfen nicht mehr als 16
zweistöckige Häuser gebaut werden. Wie ist das Grundstück zu bebauen, damit
möglichst viele Menschen auf ihm wohnen können?
Aufgabe 18:
Ein Schneider hat
50 m² Wollstoff und 37,5 m² Seidenfutter zur Verfügung. Er fertigt daraus Anzüge
und Kleider für ein Konfektionsgeschäft an. Für einen Anzug benötigt er 3 m²
Stoff und 1,75 m² Futter, für ein Kleid 2,5 m² Stoff und 2,5 m² Futter. Er will
höchstens 13 Anzüge und 10 Kleider herstellen. Sein Gewinn beträgt bei einem
Anzug 40 EUR, bei einem Kleid 50 EUR. Wie viele Anzüge und Kleider muss der
Schneider anfertigen, damit er einen möglichst hohen Gewinn erreicht?
Aufgabe 19:
Ein Elektrohändler
verkauft 2 Typen von Kühlschränken, Typ A und Typ B. Er hat sich
gegenüber dem Werk verpflichtet, monatlich mindestens 5 Geräte vom Typ A
und 8 Geräte vom Typ B zu beziehen. Aufgrund seiner Erfahrungen kann er
im Monat bis zu 30 Geräte von jedem Typ absetzen. Das Werk kann ihm jedoch für
diese Zeit höchstens 50 Geräte liefern.
a) Wie wird der
Händler zweckmäßig sein Lager bestücken, wenn der Stückgewinn bei Typ A
100 EUR, bei Typ B 150 EUR beträgt?
b) Wie ändern sich
die Mengen, wenn der Stückgewinn bei Typ A 150 EUR, bei Typ B 100
EUR beträgt?
[Sabrina Schäfer, 11b, 2004]
Aufgabe 20:
Für eine Party werden Getränke benötigt, die in
Getränkekartons verpackt werden. Karton I und Karton II (s. Abb.),
Karton I
Karton II
|
ooo
ooo A |
oooo
oooo B |
|
ooooo
ooooo
C |
|
|
oo
oo
A |
ooo
ooo B |
|
oooooo
oooooo C |
o
o
D |
|
Für die Party werden höchstens vom Bier A 20
Flaschen, Bier B 28 Flaschen und Bier C 48 Flaschen benötigt.
Außerdem werden noch mindestens 6 Flaschen von dem D Whisky benötigt. Der
Karton I kostet 50 € und der Karton II kostet 60 € ; aus Transportgründen muss
ein Karton vom Typ I mit. Die Kosten für die Kartons sollen so gering wie
möglich gehalten werden.
[Matthias Klinger, 11a, 2004]
